• Cited by: Mamou,K.: Compression de maillages 3D statiques et dynamiques, Ph.D. thesis at Université Paris V - René Descartes, France, September 2008
• Cited by: Mamou,K., Zaharia,T., Preteux,F.: FAMC: The MPEG-4 Standard For Animated Mesh Compression, Proceedings of ICIP 2008
• Cited by: Mamou,K., Stefanoski,N., Kirchhoffer,H., Muller,K., Zaharia,T., Preteux,F., Marpe,D., Ostermann,J.: The New MPEG-4/FAMC Standard for Animated 3D Mesh Compression, 3DTV Conference: The True Vision - Capture, Transmission and Display of 3D Video, 2008
• Cited by: Khan,M., Ohno,Y.: Compression of Temporal Video Data by Catmull-Rom Spline and Quadratic Bezier Curve Fitting, WSCG 2008
• Cited by: Smolic,A., Mueller,K., Stefanoski,N., Ostermann,J., Gotchev,A., Akar,G.B., Triantafyllidis,G., Koz,A.: Coding Algorithms for 3DTV-A Survey, Circuits and Systems for Video Technology, IEEE Transactions on, 2007

Achievements

We have based our efforts on the main idea of viewing the input data as a set of vertex trajectories, which must be transmitted from the encoder to the decoder. We have decided to first analyze the whole set of trajectories using the Principal Component Analysis (PCA). This analysis gives us a new basis for the space of trajectories. Each vertex is subsequently expressed in this new basis, while most of the coordinates in the new coordinate system may be neglected. This way, we achieve a 70-90% reduction of the dimensionality of the data, without losing more than one percent of the original variance of the data.

Subsequently, we use parallelogram prediction of the vertex data (i.e. PCA coefficients describing the trajectory of each vertex). This way we achieve a great reduction of the entropy of residuals. Finally, we quantize the residuals and transmit these to the decoder. This basic idea has been published in the paper CoDDyAC: Connectivity Driven Dynamic Mesh Compression.

In our following work, we have extended the algorithm by including a simplification step. Simplification by vertex decimation is performed simultaneously by encoder and decoder after transmitting connectivity data, before transmitting geometry data. The geometry data are transmitted in inverse decimation order, i.e. vertices are added into fully known neighborhoods. This process allows replacing the original extrapolation (parallelogram prediction) by interpolation, which is more precise and more robust, and therefore provides residuals of lower entropy. Moreover, the inclusion of simplification yields a scalable data stream, i.e. the decoder can stop receiving the data during the transmission and display a rough (not fully reconstructed) version of the data to the user. The enhancement by simplification is described in detail in the paper Combined Compression and Simplification of Dynamic 3D Meshes.

We have developed an advanced prediction scheme for the interpolation. The scheme is based on radial basis functions (RBF), and allows a higher precision prediction, which leads to about 25% reduction of the data rate. This approach is currently under development and has not been published yet.

We have also noticed that since the combination coefficients for the PCA can be well predicted, it is the PCA basis which takes a significant part of the compressed data stream. Knowing that the PCA basis is orthonormal, we have exploited the fact that the importance (number of times repeated in the output animation) of the basis trajectories is highly variable. Our algorithm introduces smaller quantization error to important basis trajectories and larger quantization error to less important ones. Additionally, each basis vector can be interpreted as a vertex trajectory, which we may assume to be smooth. This assumption allows using motion-based prediction of the values. Using the mentioned techniques we were able to reduce the size of the encoded basis by about 90%. These results are described in the paper COBRA: Compression of the Basis for PCA Represented Animations.

Currently we are also focusing on the problem of evaluation of the dynamic mesh compression algorithms. We have found that the currently used metrics for measuring distortion caused by lossy compression (such as MSE or DA error) are unreliable and do not correlate with human perception of distortion. Motivated by this insufficiency, we have conducted a series of subjective tests, and proposed a new metric (STED error) which provides a much better correlation with the results of subjective testing (we have obtained the Pearson correlation coefficients of about 0.95). The results of subjective testing and the proposed error metric are currently only described in the Ph.D. thesis of Libor Váša.

Results

We are presenting rate-distortion curves for two of the testing models. The rate is expressed in bits per frame per vertex, the error is computed according to Karni and Gotsman. We are comparing our algorithm (RBF + Cobra) against the current state of the art algorithm FAMC (which is now a part of the MPEG standard).

Dance model

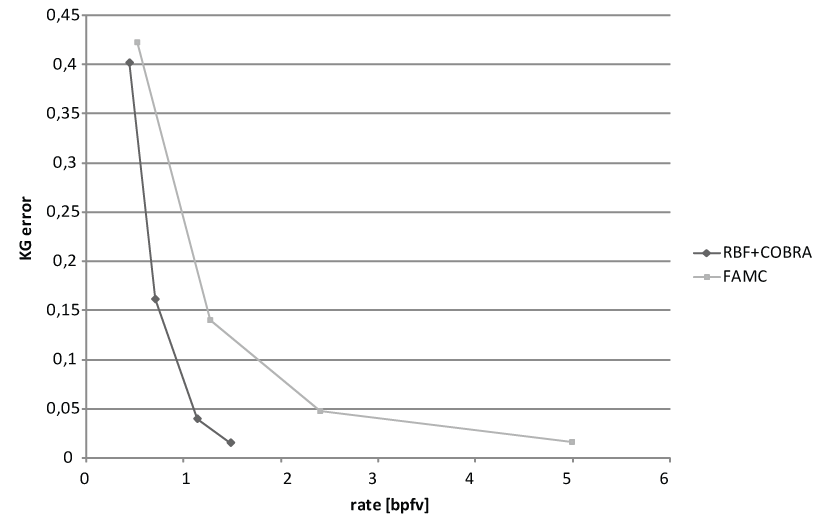
Cow model

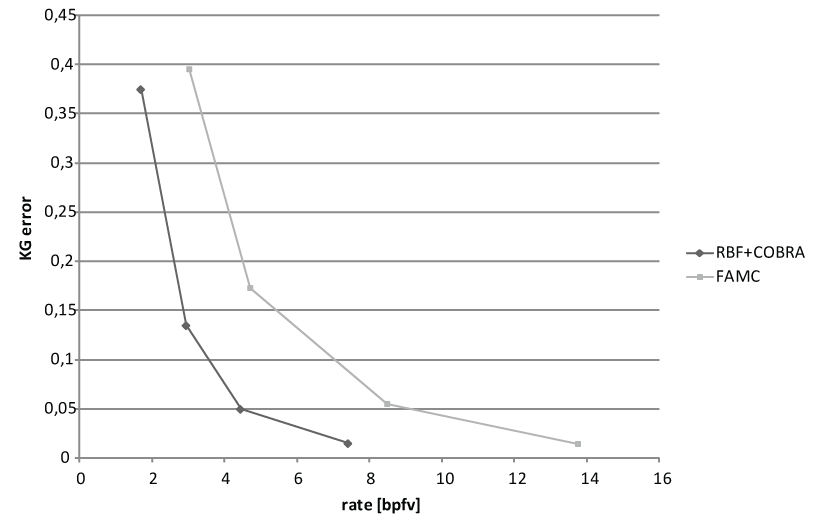
More results can found in the Ph.D. thesis of Libor Váša.

Downloads

• Loading an animation from a VRML file
• Saving an animation into a VRML file
• Comparing two animations using the KG error metric
• A torso of a compression module, which can be expanded into a new compression algorithm

Examples

A note on comparisons

There seems to be a small ambiguity in the interpretation of the KG error (for detail see Karni, Gotsman: "Compression of soft body animation sequences"). Therefore we are presenting a piece of source code in C# which demonstrates how the KG error should be computed. Please note that this interpretation is a consensus of several researchers in the field of dynamic mesh compression.

int pointCount = ((UnstrGrid)input1[0]).Points.Count;
int frameCount = input1.Count;

double[,] means = new double[frameCount, 3];
for (int i = 0; i < pointCount; i++)
{                    
    for (int j = 0; j < frameCount; j++)
    {
        TriangleMesh mesh = (TriangleMesh)input1[j];
        Point3D point = (Point3D)mesh.Points[i];
        means[j, 0] += point.X;
        means[j, 1] += point.Y;
        means[j, 2] += point.Z;
    }
}
for (int i = 0; i < frameCount; i++)
{
    means[i, 0] /= pointCount;
    means[i, 1] /= pointCount;
    means[i, 2] /= pointCount;
}

double s1 = 0;
double s2 = 0;

for (int i = 0; i < frameCount; i++)
{
    UnstrGrid frame1 = (UnstrGrid)input1[i];
    UnstrGrid frame2 = (UnstrGrid)input2[i];

    UniformDataArray points1 = frame1.Points;
    UniformDataArray points2 = frame2.Points;                    
    for (int j = 0; j < pointCount; j++)
    {
        Point3D p1 = (Point3D)points1[j];
        Point3D p2 = (Point3D)points2[j];      
        s1 += (p1.X - p2.X) * (p1.X - p2.X);
        s1 += (p1.Y - p2.Y) * (p1.Y - p2.Y);
        s1 += (p1.Z - p2.Z) * (p1.Z - p2.Z);
        s2 += (p1.X - means[i, 0]) * (p1.X - means[i, 0]);
        s2 += (p1.Y - means[i, 1]) * (p1.Y - means[i, 1]);
        s2 += (p1.Z - means[i, 2]) * (p1.Z - means[i, 2]);
    }
                        
}
result = new Scalar((Math.Sqrt(s1)/Math.Sqrt(s2))*100);                

SetOutput("KG error", result);